定义
非确定型有穷自动机(NFA),在某状态下,对于指定的输入,存在多个转移状态。一般情况下,通过某种算法可转换为 DFA
上下文无关文法 描述程序设计语言的结构以及相关集合的重要记号,用来构造编译器的语法分析部件。
字母表 符号的有穷非空集合。用表示
串(有时候称为单词)是从某个字母表中选择的符号的有穷序列。例如 01101 是从二进制字母表中选出的串
空串 出现 0 次符号的串,记做
串的长度 这个串中的符号数,记做,例如
字母表的幂 定义是长度为 k 的串的集合。串的每个符号都属于。无论是什么字母表。字母表上所有的串的集合约定为,排除空串的集合约定为
串的连接 设定 x 和 y 都是串,于是 xy 表示 x 和 y 的连接
集合表示法 的语义描述。比如包含相同个数的 0 或 1,还可以把换成某个带参数的表达式
当两个状态机交互时,当其状态处于,对于一个合法的输入,可使,,那么我们可以认为是可达的
确定型有穷自动机(DFA)
确定型有穷自动机 包含若干个状态的集合,若干个输入符,当有输入时,控制权将由一个状态转移到另一个状态。在任意状态下,对于指定的输入,其转移是唯一的。
一个有穷状态集合,记做,
初始状态记做,
终止状态记做
一个有穷输入集合,记做
状态转移函数,记做,以一个状态和一个输入符号作为参数,返回一个状态。
- 扩展状态转移函数,记做,以一个状态和一个输入串作为参数,返回一个状态。
- 假定,a 是最后的输入,
DFA 的定义:
对于所有 DFA,我们可以定义为
例如出现 01 字符串可能出现三个状态
- 未遇到 01,且最后一个不为 0,
- 未遇到 01,且最后一个为 0,
- 已遇到 01,可接受任意 0 或 1,
其 DFA 表达式:
对 DFA 的细节描述难以阅读,通常使用两种方式来更好的描述
状态转移图
graph LR; begin( )-->|Start|q0 q0-->|0|q1 q0-->|1|q0 q1-->|0|q1 q1-->|1|q2 q2-->|0,1|q2 style begin color:white,fill:white,stroke:white
状态转移表,一个状态和输入组成的的表
0 1
使用扩展转移函数,对一个串 0011 进行计算
这种方式的处理,非常适合我们用递归函数进行计算。
非确定型有穷自动机(NFA)
与确定型有穷自动机类似,包含若干个状态,若干个输入符,状态转移函数,终止状态。唯一不同的是,的结果可能是零个、一个、或多个状态的集合。
一个有穷状态集合,记做,
初始状态记做,
终止状态记做
一个有穷输入集合,记做
状态转移函数,记做,以一个状态和一个输入符号作为参数,返回一个状态。
- 扩展状态转移函数,记做,以一个状态和一个输入串作为参数,返回一个状态。
- 假定,,那么
对于 NFA,可以定义为
例如,以 01 结尾
其状态转移图如下
graph LR; begin( )-->|Start|q0 q0-->|0|q1 q0-->|0,1|q0 q1-->|1|q2 style begin color:white,fill:white,stroke:white
当接受到 0 时,NFA 会猜测最后的 01 已经开始了,一条弧线从指向,我们可以看到 0 有两条弧线,另一条指向。NFA 会同时走这两条线。当在状态时,它会检查下一个符号是否为 1,如果是则会进入状态。当在状态时,如还有其他输入,这条路线就终结掉了。
00101 的处理过程如下 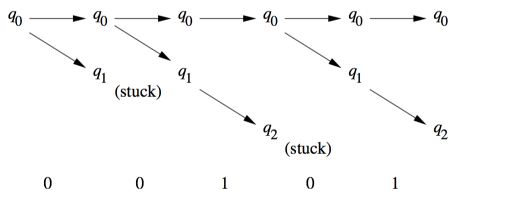
其状态转移表如下
| 0 | 1 | |
|---|---|---|
| * |
使用扩展转移函数的处理过程如下
NFA 与 DFA 的转换
通常来说,构造 NFA 比构造 DFA 更容易,每一个用 NFA 描述的语言也能用 DFA 来描述。这个可以用子集构造来证明。
子集构造从一个 NFA 开始,转换为
- 两个自动机的输入字母表是相同的
- D 的起始状态为仅包含 N 的起始状态的长度为 1 的集合
- 是子集的集合,即幂集合。假如有 n 个状态,那么有状态,通常不是所有的状态都是从可达的,这些状态可以丢弃,所以实际上的状态要远远小于
- 所有满足的的子集的集合 S,也就是说,是状态子集中至少包含一个的集合。
- 对于的集合 S 中每个状态来说,其对应的每个属于的输入符号的转移函数为:
示例,我们以接受所有 01 结尾的串的 NFA 向 DFA 转换,由于,所以子集构造产生一个带有(并非所有状态都是有意义的)种状态的 DFA
| 0 | 1 | |
|---|---|---|
| 0 | 1 | |
|---|---|---|
| A | A | A |
| E | B | |
| C | A | D |
| A | A | |
| E | E | F |
| E | B | |
| A | D | |
| E | F |
从状态 B 开始,只能到达状态 B、E 和 F。其余五种状态都是从初始状态不可达的,也可以不出现在表中。如果向下面这样在子集合中执行惰性求值,通常就能避免以指数时间步骤为每个状态子集合构造转移表项目。一般情况下,我们可以从初始状态 A 开始计算可到达状态,若有新的可达状态,我们继续计算,直到没有新的可达状态。
graph LR; begin( )-->|Start|B B-->|0|E B-->|1|B E-->|0|E E-->|1|F F-->|0|E F-->|1|B style begin color:white,fill:white,stroke:white
我们需要证明这个子集构造是正确的。
在读入输入符号序列后,所构造的 DFA 处于这样一个状态,这个状态时 NFA 在读后所处的状态的集合。由于 DFA 的接受状态是至少包含一个 NFA 接受状态的集合,因为包含 NFA 的可接受状态,因此这个集合也是被 NFA 接受的。于是我们可以得出结论,这个 DFA 和 NFA 接受完全相同的语言。
我们来证明 若是从子集构造出来的,那么,这也就是证明,对于输入字母表 ,
当,即,根据的定义, 的结果都为
假定 ,,,成立,两个集合状态 N 为。
那么对于 NFA:
通过子集构造的定义我们可以得出
又因
文本搜索
识别 web 和 ebay 出现
通过 NFA 来实现 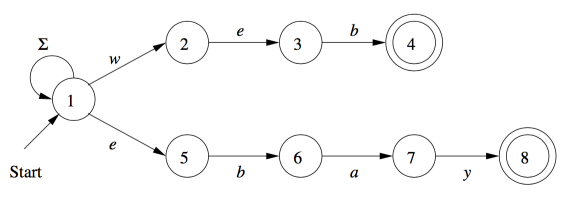
对终止状态[4,8]增加了回到1的转移,以支持 web 和 ebay 出现在中间位置。
1 | //识别单词web和ebay出现的NFA |
通过子集构造的方式来转换为 DFA,省略[4,8]的1出口 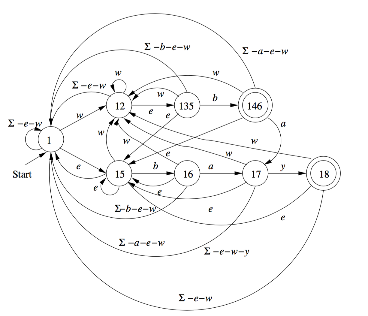
1 | //状态转移函数 |
上述输出结果为,与例图完美对应
1 | { |